
 Numerical Methods for Partial Differential Equations
Numerical Methods for Partial Differential Equations
CS555 :: Spring 2025
- Class Time: Tuesday/Thursday 12:30-1:45pm [Catalog]
- Class Location: 1035 Campus Instructional Facility (CIF)
- Class URL: go.illinois.edu/cs555
- Instructor: Luke Olson
- About the Course
- Lectures
- Homework
- Final Project
- On COVID and Attendance
 About the Course
About the Course
Are you interested in the numerical approximation of solutions to partial differential equations? Then this course is for you!
The course covers roughly three topics: the fundamentals of finite difference approximations, an introduction to finite volume schemes, and comprehensive look at finite element methods.
 Prerequites
Prerequites
The expectation is that you have had a course in numerical methods (like CS450), covering conditioning, numerical linear algebra, numerical quadrature and differentiation, and the basics of numerical methods for ordinary and differential equations. If you do not have this background, please check with the instructor.
In addition, you should have some familiarity with Python. All example, homeworks, and the project will be conducted in Python. If you do not have this background, please check with the instructor.
The course will take a deep look at the mathematical underpinning of the methods used to approximate solutions to partial differential equations. If you have questions about your mathematical preparation for this course, please check with the instructor.
 Expected work
Expected work
The course involves several assignments and a final project that we develop over the semester, culminating in a presentation. There is also a strong participation grade based on quizzes, handouts, and other in-class tasks. The tentative grade breakdown is:
- Homework 40
- Final Project 40
- Quizzes, in-class work 20
This will be finalized in the first week of class.
The course assignments and examples in class will be in Python.
 Lectures
Lectures
Recorded Lectures: mediaspace.illinois.edu
| Lecture | Date | Topic | |
|---|---|---|---|
 |
01-21 | About the course, classifying PDEs, survey of methods
|
|
 |
01-23 | Finite differencing for time dependent problems
|
|
 |
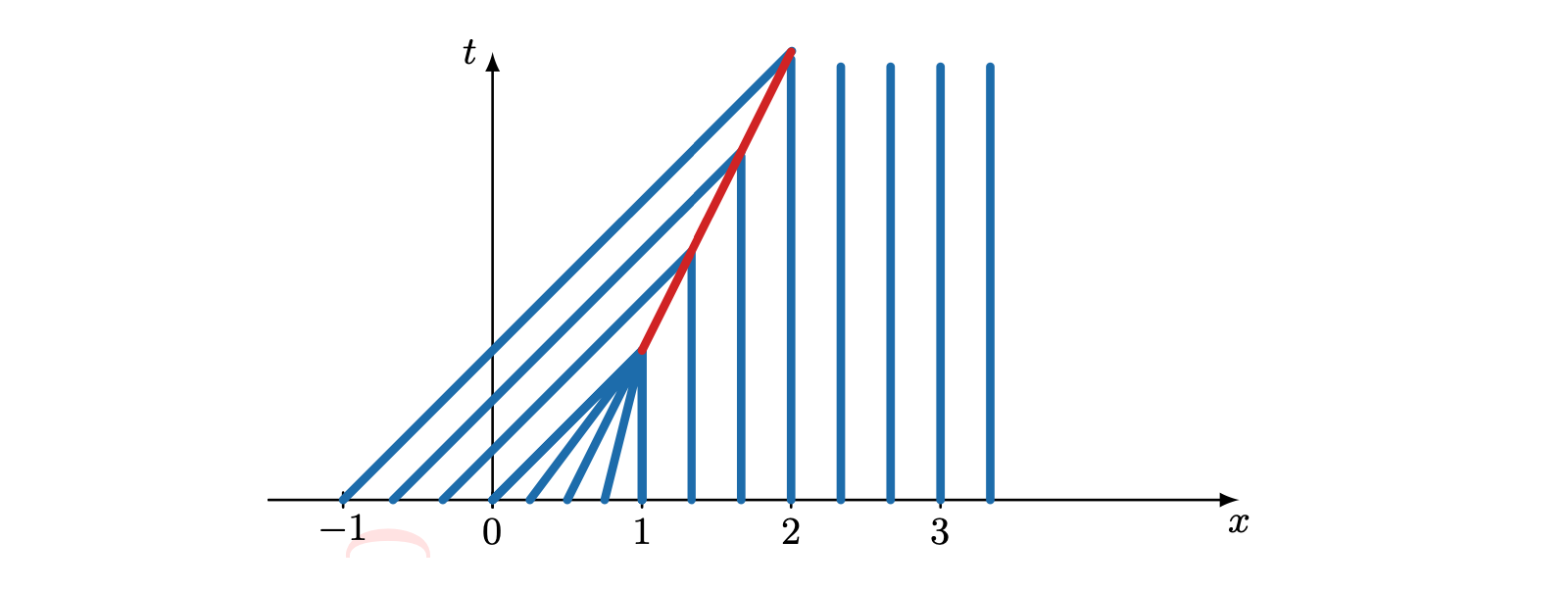
01-28 | Convergence theory, Stability
|
|
 |
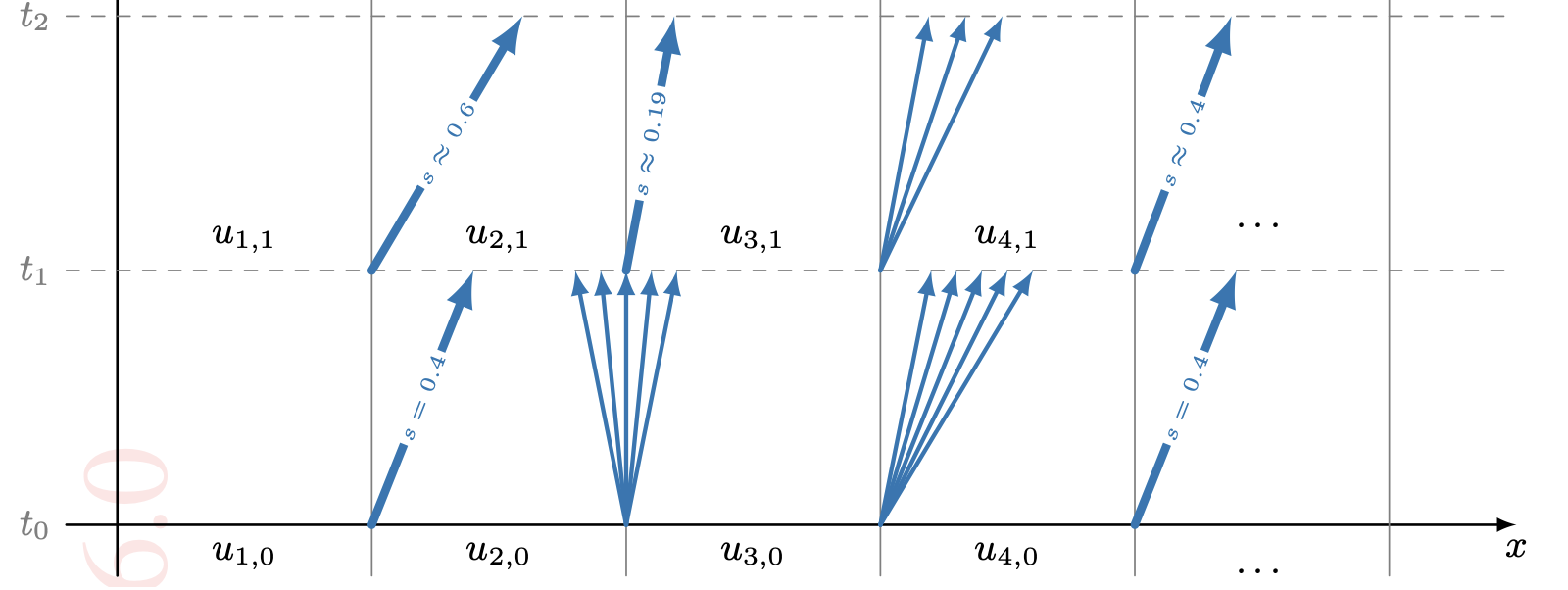
01-30 | von Neumann Stability
|
|
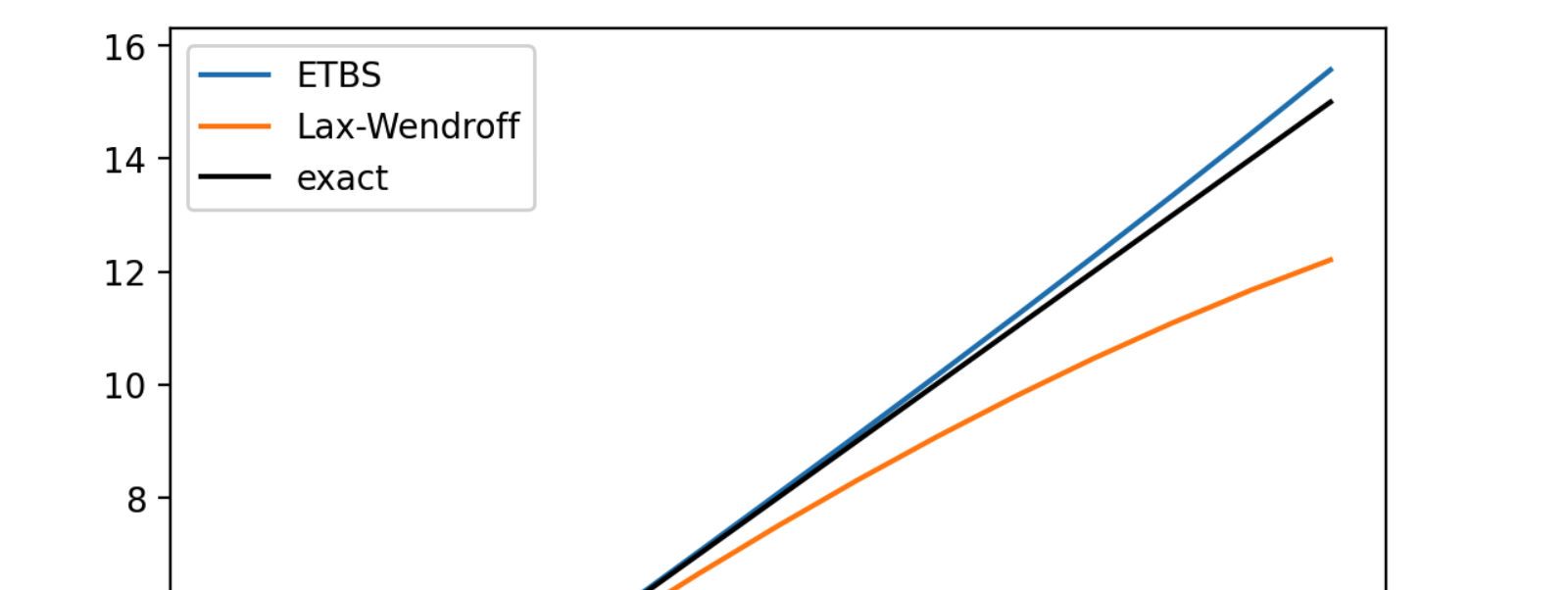 |
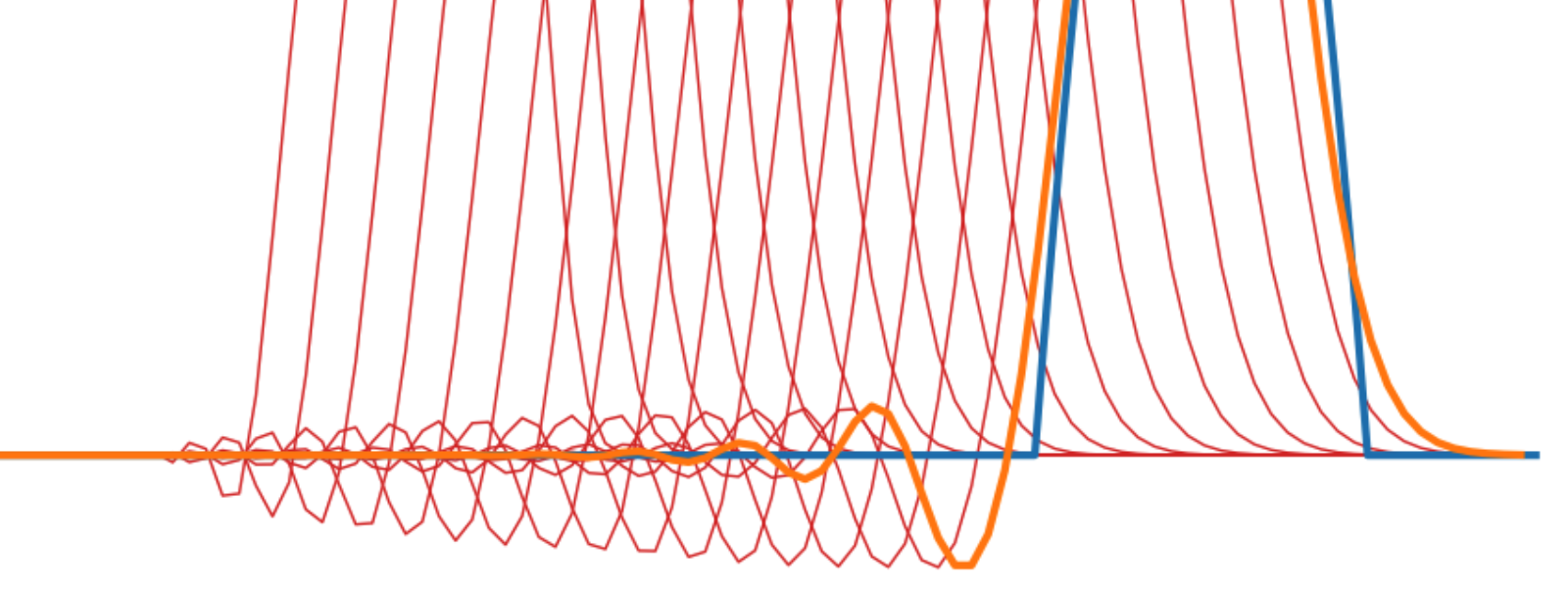
02-04 | Dispersion, and dissipation
|
|
 |
02-06 | Conservation laws, finite volume methods
|
|
 |
02-11 | Finite Volume Methods
|
|
 |
02-13 | Godunov Schemes
|
|
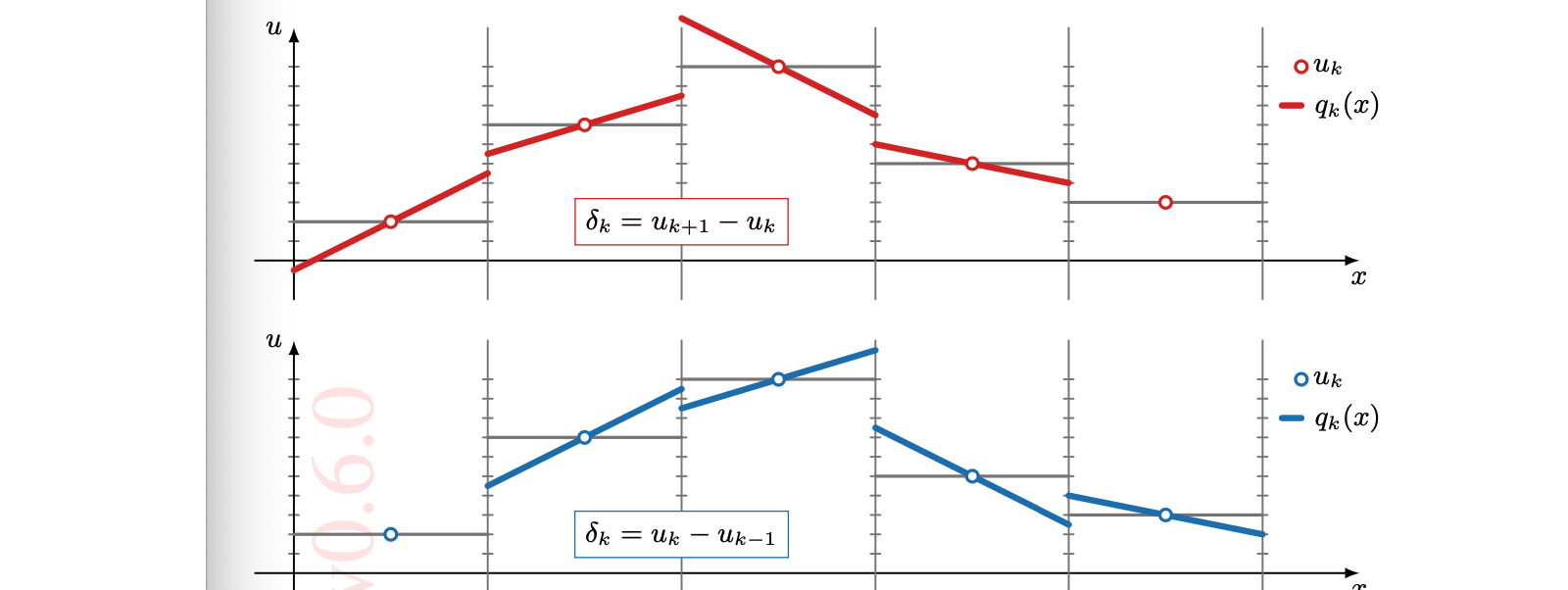 |
02-18 | Higher resolution and slope limiting
|
|
 |
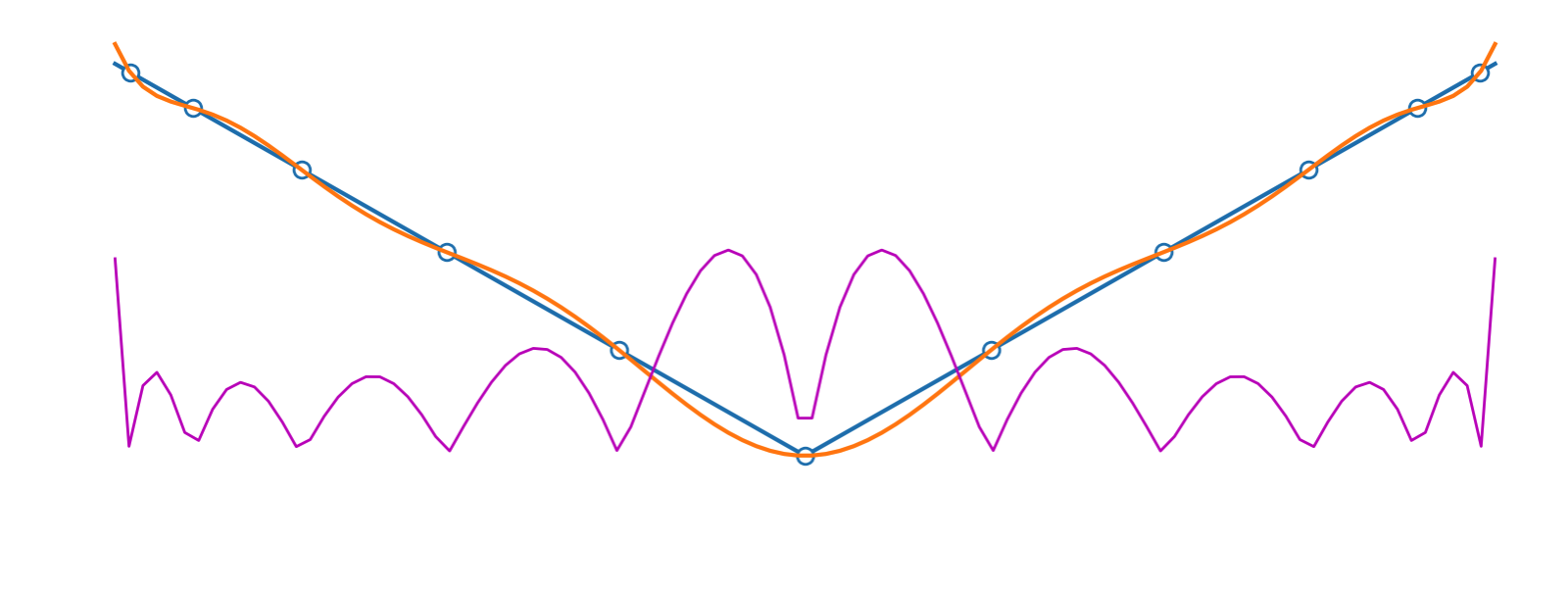
02-20 | Higher resolution and slope limiting | |
 |
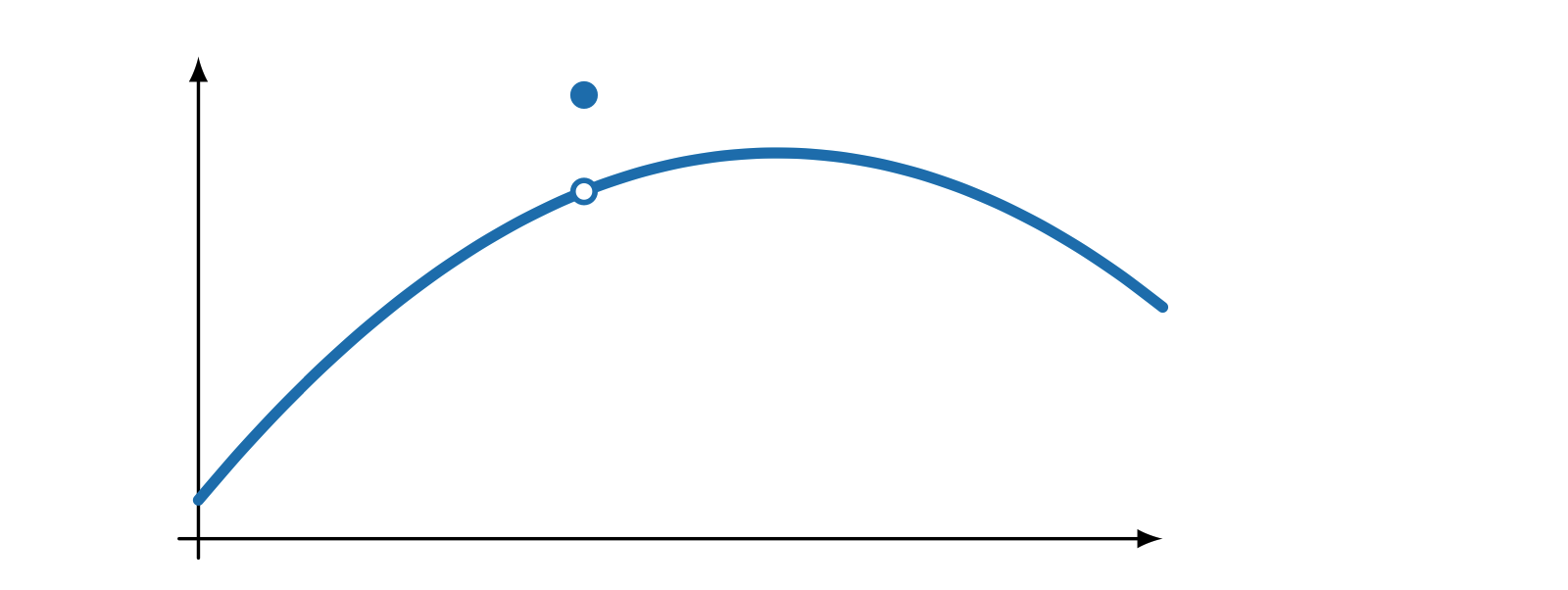
02-25 | Projections, weak problems, weak derivatives
|
|
 |
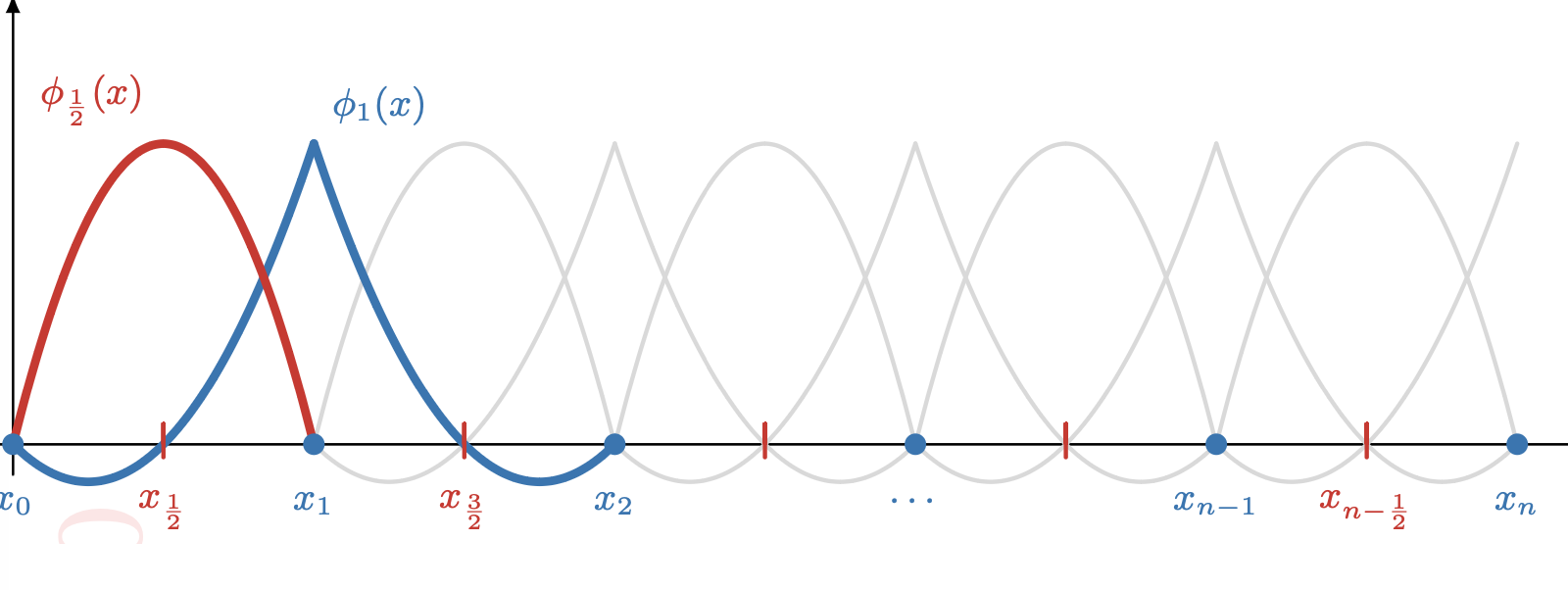
02-27 | Weak forms, Ritz-Galerkin, existence and uniqueness
|
|
 |
03-04 | Finite element assembly
|
|
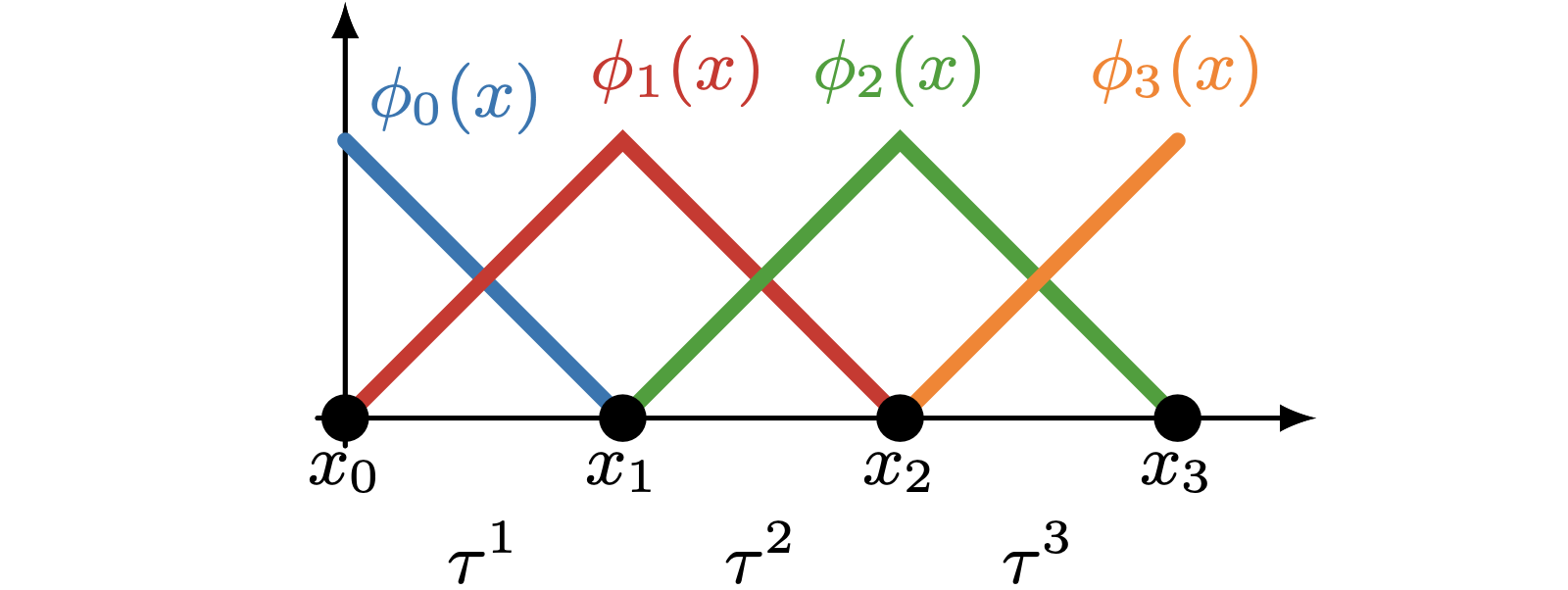 |
03-06 | Finite element interpolant, approximation property
|
|
 |
03-11 | Various FE methods, from least-squares to Galerkin
|
|
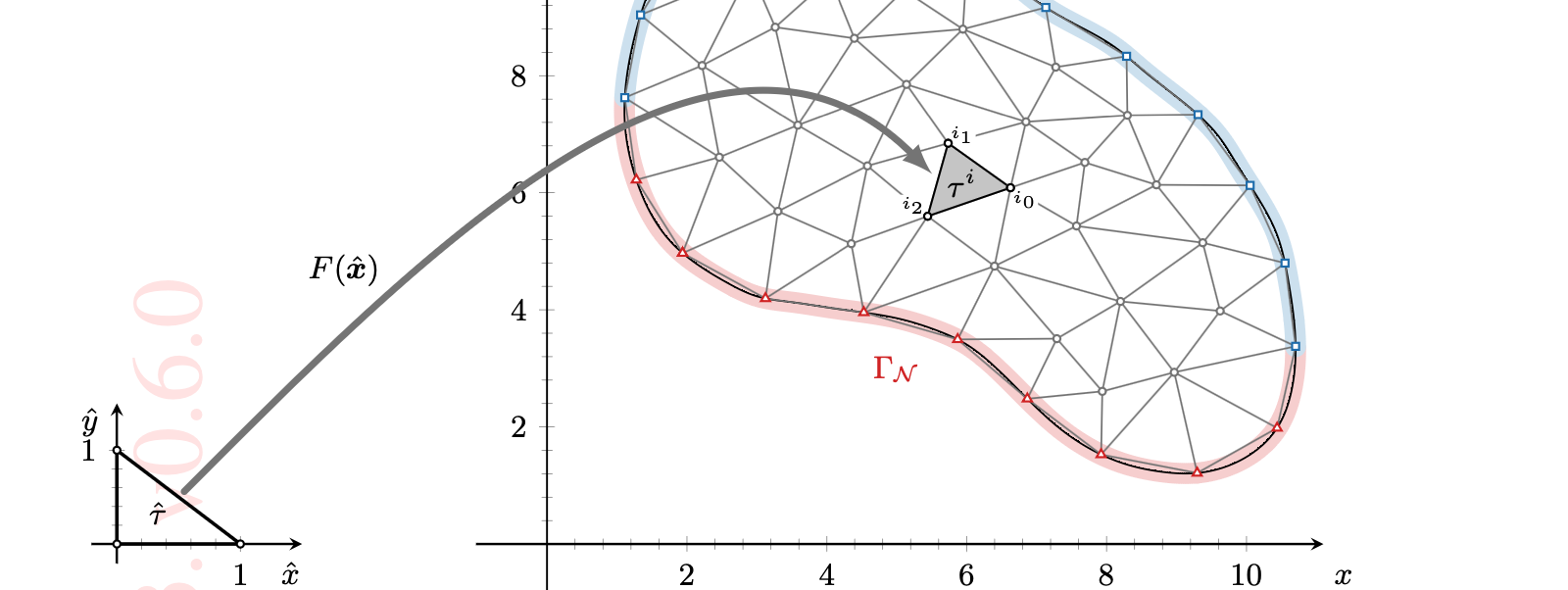 |
03-13 | Finite element assembly in 2D
|
|
| 03-18 |
|
||
| 03-20 |
|
||
 |
03-25 | Project Overview | |
 |
03-27 | Introduction to Functional Anaylsis
|
|
 |
04-01 | An outline of theory, Lax-Milgram, and more
|
|
 |
04-03 | Back to DG, conservation laws
|
|
 |
04-08 |
|
|
 |
04-10 | DG elliptic
|
|
| 04-15 | Multigrid
|
||
| 04-17 |
|
||
| 04-22 |
|
||
| 04-24 |
|
||
| 04-29 |
|
||
| 05-01 |
|
||
| 05-06 |
|
||
| 05-08 |
|
 Homework
Homework
- Homework 1, Due: Friday, Feb. 14, 6pm
- Homework 2, Due: Tuesday, March 04, 6pm
- Homework 3, Due: Monday, March 24, 6pm
- Homework 4, Due: Friday, April 4, 6pm
Guidelines and files:
- Homework Submission: All homework must be typeset using LaTeX. Use the provided templates to get started, available at homework-netid-N.tex org overleaf.
- Figures: Make sure all figures are clearly labeled with axes, titles, legends, and captions. Each figure must be referenced and discussed within your text for full credit.
- Originality: Your submitted code and figures must be your own. If you use someone else's work, you must cite it.
- Code-Based Problems: To receive points for problems involving code, your code must reproduce the reported figures and data. No points will be awarded for the Codes that do not generate the reported results.
- Debugging Efforts: If you encounter issues that prevent your code from working as expected, detailed descriptions of your debugging attempts can earn you partial credit.
 Final Project
Final Project
The goal of the final project is to develop your own mini app -- a short computational example of some phenomenon in numerical PDEs. This can be related to any of the topics covered, from finite differencing to finite volume methods to finite element methods. An overarching goal of your mini app is to educate your peers on some nuanced aspect of the topics we have covered (or have skipped).
Your deliverables for the project will be a functioning Jupyter notebook, with an embeddeed description, discussion, and guide for the audience. In addition, you will present an overview of up to five minutes (with slides).
The mini app should rely only on standard Python, along with numpy, scipy, and matplotlib. If you strongly feel that you should use additional packages, please obtain prior approval.
The rubrics for the mini app are as follows.
SP, Statement of problem
- What is the problem that you are looking at? What is the is point of the the mini app? What interesting aspect of numerical PDEs does your mini app highlight?
- Is the problem clear? Have you provided enough background information for the audience to follow?
ID, Implementation details
- Is your example well documented?
- Is your mini app reproducible with minimal effort?
- What details are needed to understand the implementation?
- Is your Python code style clean and Pythonic? (see for example, The Zen of Pytyhon, https://peps.python.org/pep-0020/)
R, Results
- Do your results highlight the overarching goal of your mini app?
- What do you observe for this problem and discretization, for example?
- Are your results clear? Do you label important details? Do you use relevant and consistent color schemes?
- Carefully select which visualizations to show. We do not need to see everything, only figures that highlight some aspect of the goal of your mini app.
C, Reflections
- What did you learn? What worked, what needs improvement, what are the next steps or future directions?
- Provide a list of future directions at the end of your app -- what could be looked at next and what are some of the limitations of your implementation?
Slides should focus on
- (3) Do you have a clear summary and goals of your miniapp?
- (2) Do you provide a sufficient level of detail in showing off your mini app?
- (2) Do you highlight a few (but not all) of the results in your mini app?
- (3) Is your presentation practiced and on time? Is your slide deck of high quality?
| project step | description | points | due |
|---|---|---|---|
| project 0 | idea | 2 | Th 3/27 |
| project 1 | outline | 2 | Th 4/3 |
| project 2 | results | 2 | Th 4/10 |
| project 3 | results | 3 | Th 4/17 |
| project 4 | mini app (notebook) | 20 | Tu 4/29 |
| project 5 | slides | 10 | Tu 4/29 |
| project 6 | pick a license | 1 | Tu 4/29 |
| total | 40 |
Code details.
- The code should be your own. If you use someone else's function or module, then it should be clearly attributed and the license should conform to your license.
- License. Ideally it would be useful if your mini app is released as open source.
- Your notebook should be named
miniapp_topic.ipynb. No spaces or dashes.
 COVID and Attendance
COVID and Attendance
While face coverings are not required in classrooms (current as of 12/20/2023) we fully support your decision to wear one if you wish.
If you test positive for COVID, then you should not attend class.
If you have any cold-like symptoms or do not feel well, then you should not attend class, regardless of testing negative or positive for COVID.
In either case, your missed attendance due to illness will not impact your grade in the course and we will work with you to cover the material missed in class (via Zoom).
