Numerical Methods for Partial Differential Equations

CS555 :: Spring 2023

• Class Time: Monday/Wednesday 11:00am-12:15pm Catalog
• Class Location: 1035 Campus Instructional Facility (CIF)
• Class URL: go.illinois.edu/cs555
• Slack: cs555-s23
• Instructor: Luke Olson
• Teaching Assistant: Alexey Voronin
• Office Hours: Mondays 4-5pm and Thursdays 4.30-5.30pm via zoom (NetID signin)

About the Course

Are you interested in the numerical approximation of solutions to partial differential equations? Then this course is for you!

The course covers roughly three topics: the fundamentals of finite difference approximations, an introduction to finite volume schemes, and comprehensive look at finite element methods.

The course involves several assignments (usually bi-weekly) and a final project that we develop over the semester, culminating in a presentation. There is also a strong participation grade based on handouts and other in-class tasks. The tentative grade breakdown is:

• Homework 50
• Final Project 30
• Handouts/in-class activities 20 (we will be clear about these -- not all will be handed in)

This will be finalized in the first week of class.

The course assignments and examples in class will be in Python.

Lectures

lecture zoom videos

Lecture	Date	Topic
	01-18	About the course, classifying PDEs, survey of methods Book Chapter 1 notes-0118.pdf
	01-23	Finite differencing for time dependent problems Book Sections 2.2, 3.1, 3.3, 5.1-5.3 05-advection-1d.ipynb  notes-0123.pdf
	01-25	Convergence theory, Stability Book Sections 5.1-5.3 notes-0125.pdf
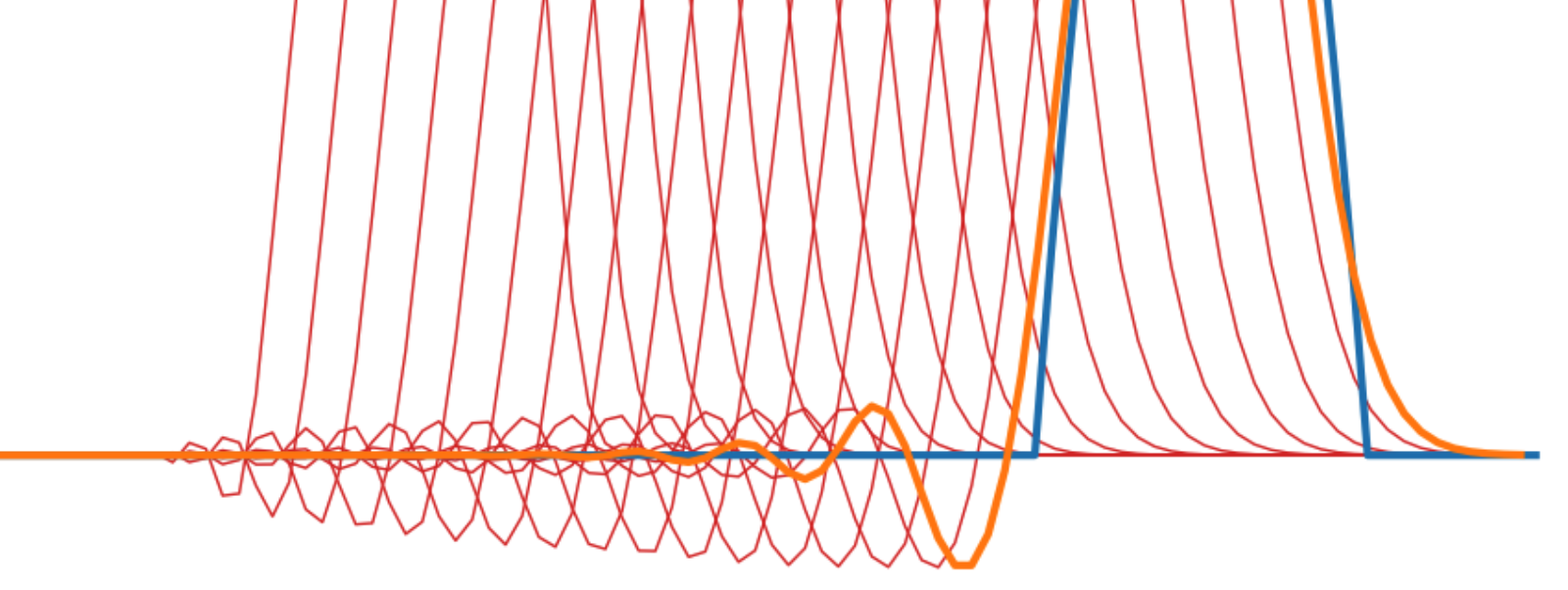	01-30	Stabilty, dispersion, and dissipation Book Sections 5.1-5.4 05-advection-ETBS-LW.ipynb  notes-0130.pdf
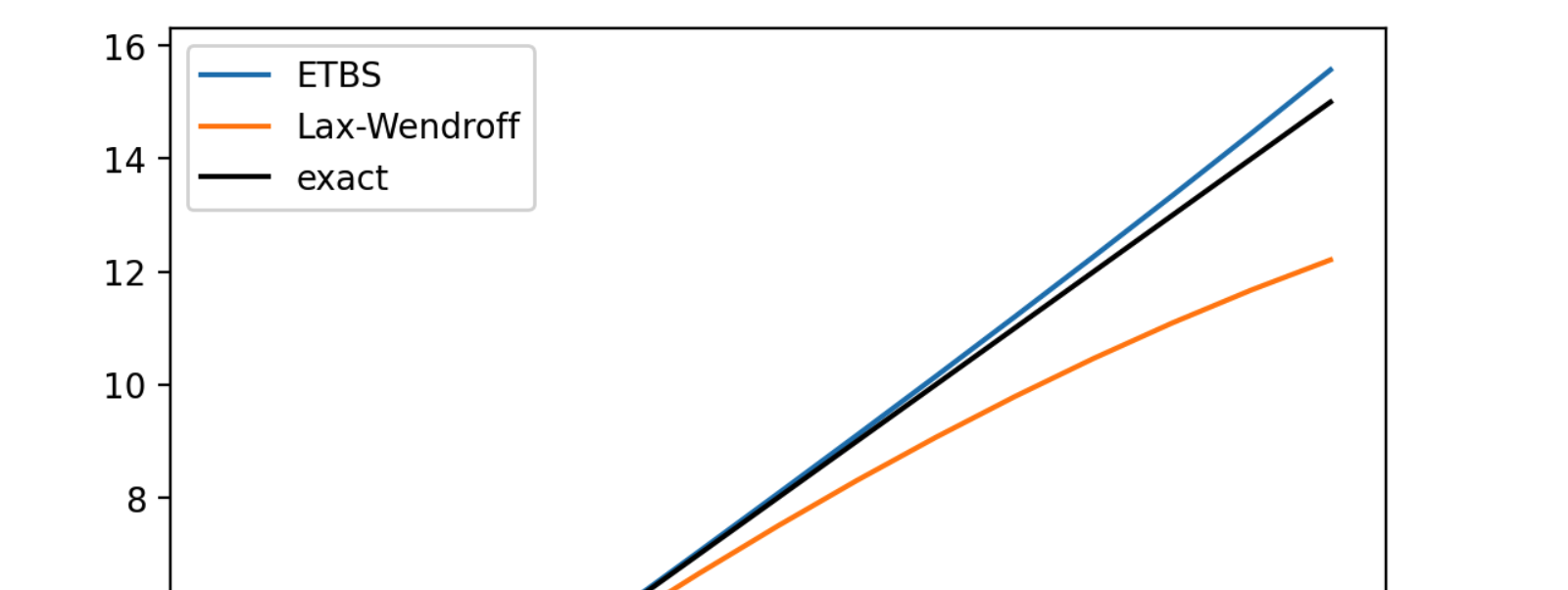	02-01	Dispersion, and dissipation Book Sections 5.3-5.4 Scalar conservation laws 05-advection-ETBS-LW.ipynb  05-dispersion-and-dissipation.ipynb  notes-0201.pdf
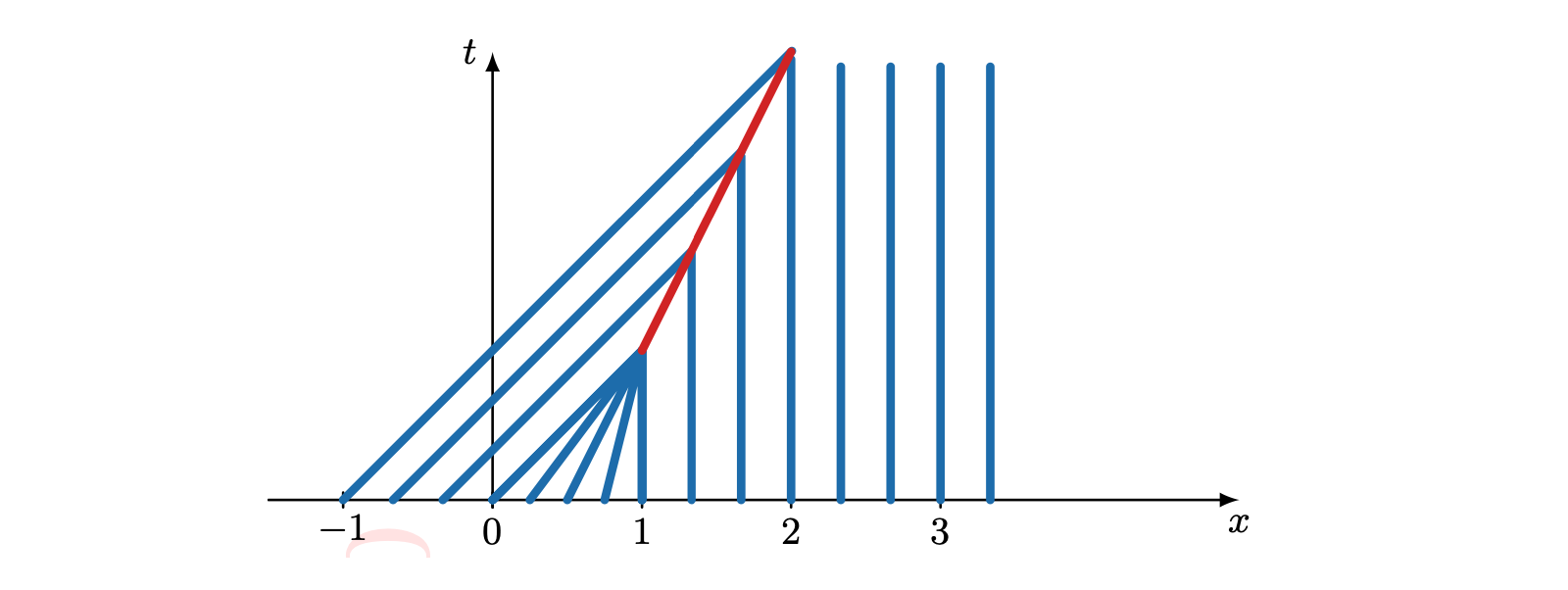	02-06	Conservation laws, finite volume methods Book Sections 6.1-6.2 06-burgers-ETBS.ipynb  06-burgers-fv-1storder.ipynb  handout-conservation.pdf notes-0206.pdf
	02-08	Finite Volume Methods Book sections 6.2-6.3 06-quasilinear-advection.py (raw) notes-0208.pdf
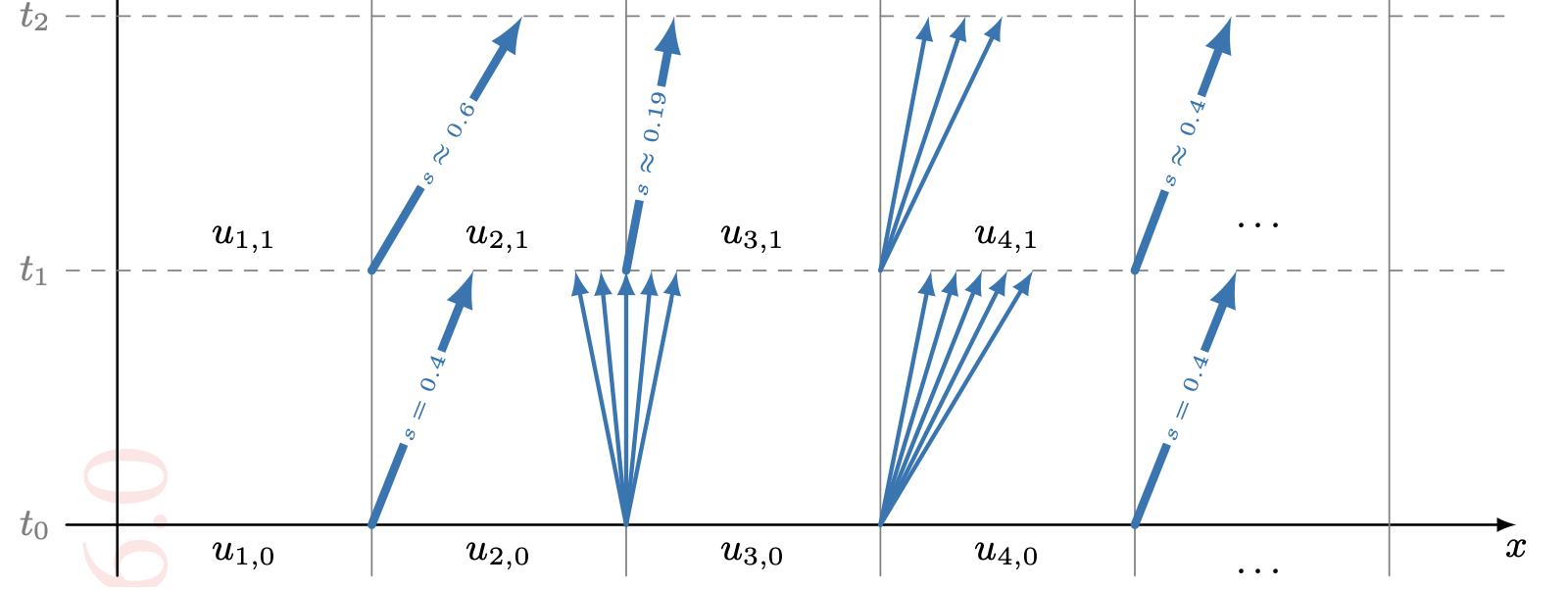	02-13	Godunov Schemes Book sections 6.3, 6.5 06-quasilinear-advection.py (raw) 06-quasilinear-advection-linear.py (raw) 06-burgers-LF-template.ipynb  notes-0213.pdf
	02-15	Higher resolution and slope limiting Book sections 6.5 06-advection-linear.py (raw) notes-0215.pdf
	02-20	Total Variation Diminishing Book sections 6.5 06-quasilinear-advection-linear-tvd.py (raw) 06-quasilinear-advection-linear.py (raw)
	02-22	Multiple variables Book sections 9.2 notes-0222.pdf
	02-27	Multiple dimensions Book sections 9.3 09-hyperbolic-2d.py (raw) notes-0227.pdf
	03-01	Discontinuous Galerkin for conservation laws Book sections 9.6 09-burgers-dg.py (raw) notes-0301.pdf
	03-06	Discontinuous Galerkin for conservation laws, implementation Book sections 9.6 09-burgers-dg.py (raw) nodal-modal.ipynb  notes-0306.pdf
	03-08	Projections polynomial-approximation-template.ipynb  2-polynomial-approximation.ipynb  project info: cs555-project-information.pdf notes-0308.pdf
	03-13	Spring Break
	03-15	Spring Break
	03-20	Weak forms, Ritz-Galerkin, existence and uniqueness Book Section 4.1, 4.2
	03-22	Finite element interpolant, approximation property Book section 4.3 project 0: Project selection + peer feedback
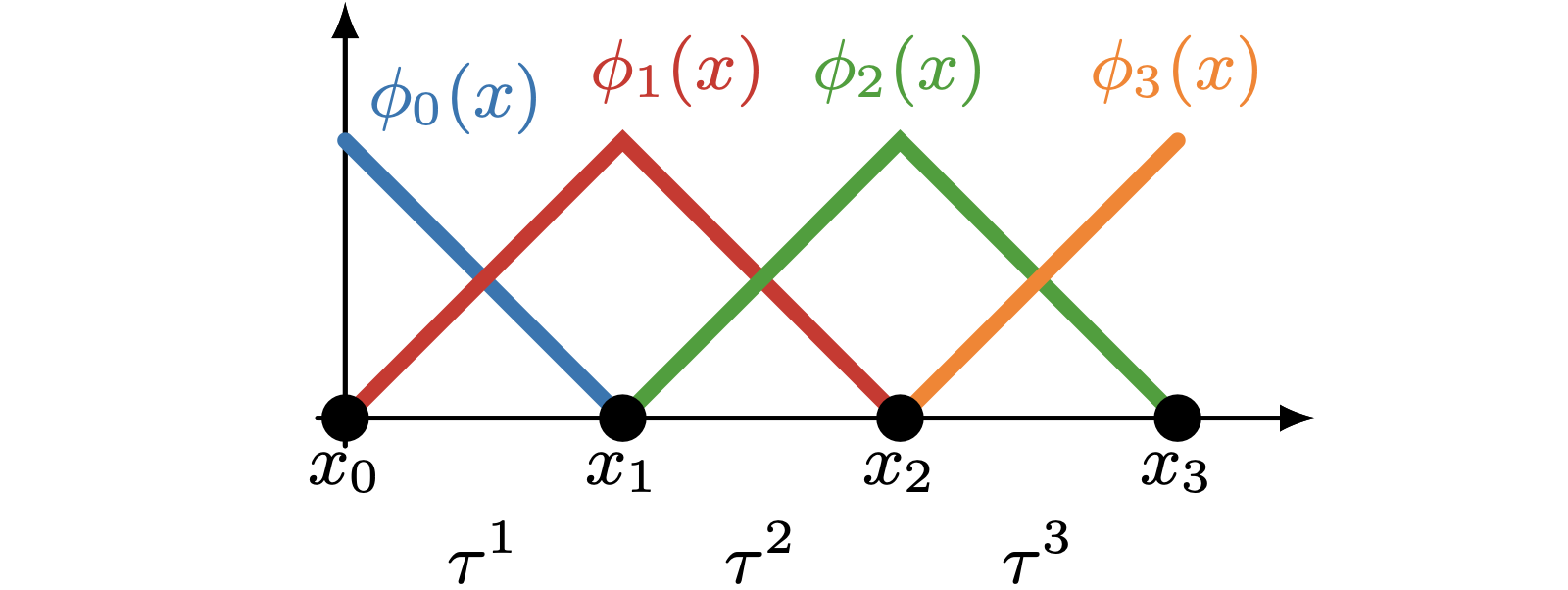	03-27	Finite element interpolant, approximation property Finite element assembly, 1d Book section 4.4 notes-0327.pdf
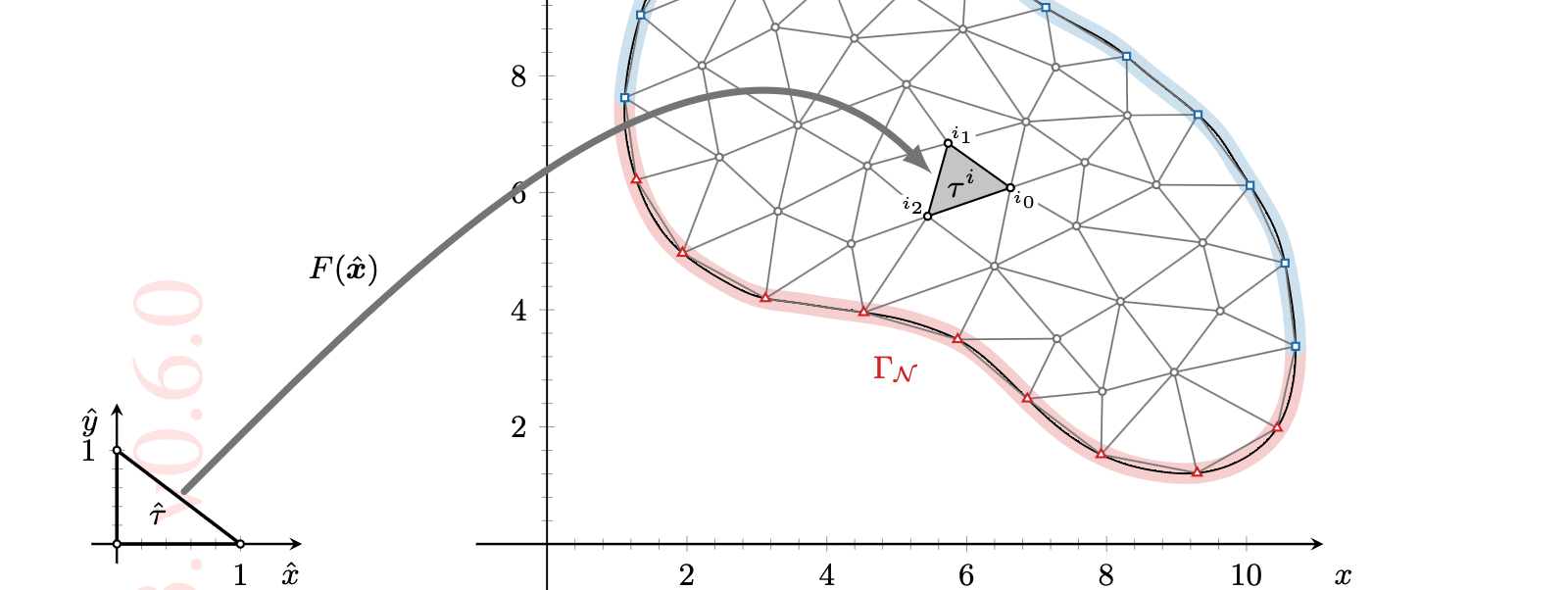	03-29	Finite element assembly Book section 8.4 project 1: Project goals, workflow, reference source, a list notes-0329.pdf 08-fe-assembly.ipynb
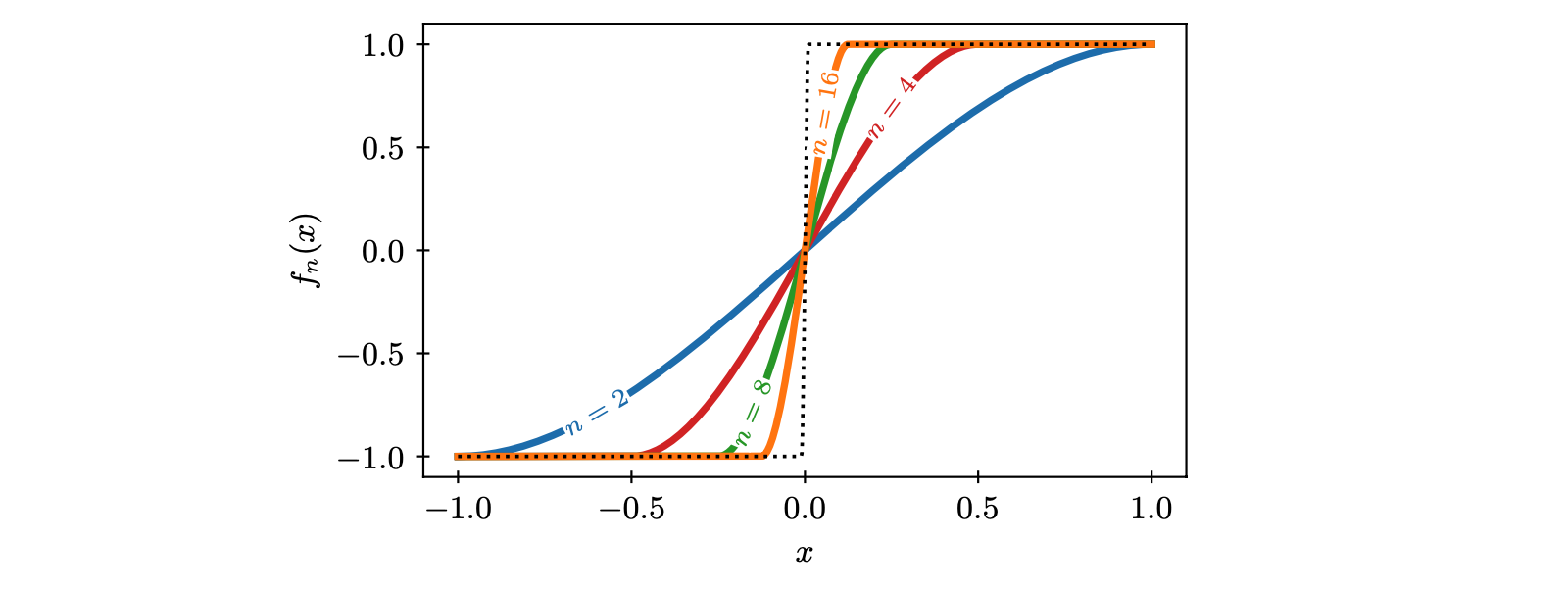	04-03	An overview of spaces Book section 8.1 Intro to Firedrake helmholtz_modified.ipynb
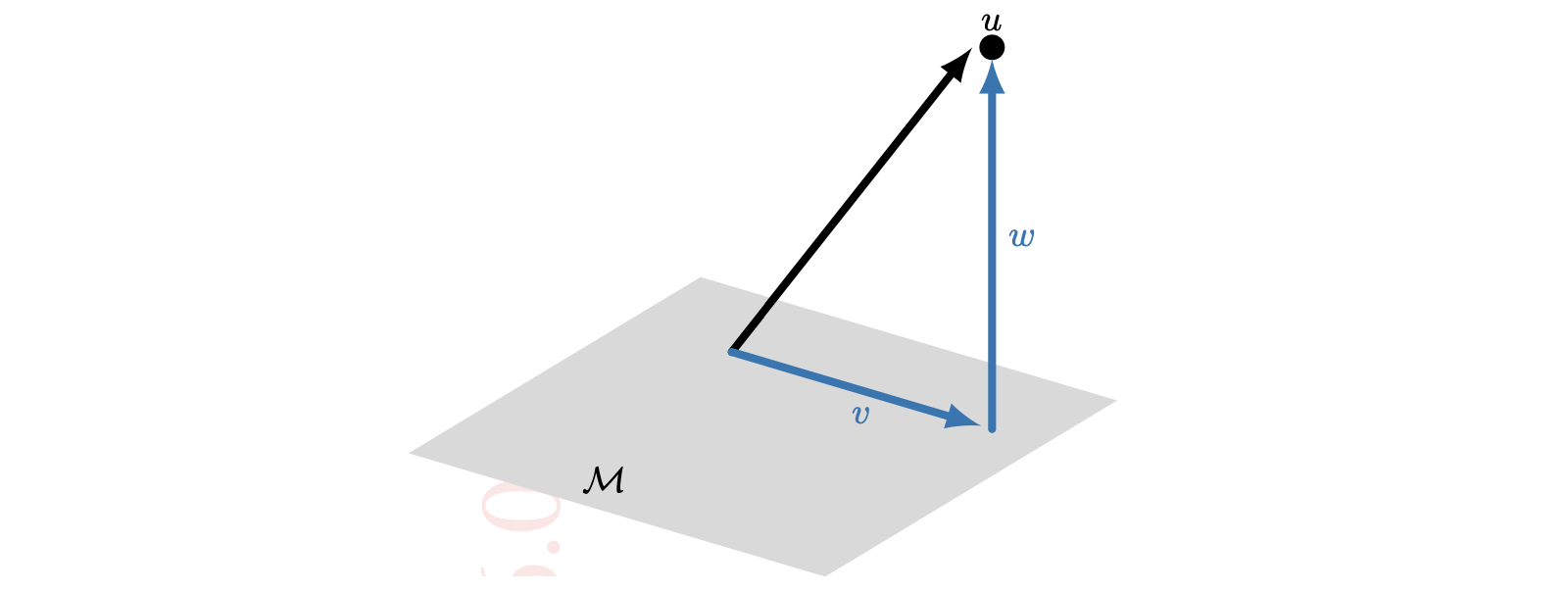	04-05	An outline of theory, Lax-Milgram, and more Book section 8.2 notes-0405.pdf project 2: Project outline
	04-10	An outline of theory, Lax-Milgram, and more Book section 8.2 notes-0410.pdf
	04-12	Finite elements and approximation properties Book section 8.3 notes-0412.pdf project 3: Project initial results
	04-17	Back to DG Book section 9.5 notes-0417.pdf
	04-19	no class 555-presentation.pdf project 4: Project initial results
	04-24	Least-squares finite elements Book section 10.5
	04-26	project: Presentations, day 0 project 5: Project slides due Presentation 0.0 -- TBD Presentation 0.1 -- TBD Presentation 0.2 -- TBD Presentation 0.3 -- TBD Presentation 0.4 -- TBD Presentation 0.5 -- TBD Presentation 0.6 -- TBD
	05-01	project: Presentations, day 1 Presentation 1.0 -- TBD Presentation 1.1 -- TBD Presentation 1.2 -- TBD Presentation 1.3 -- TBD Presentation 1.4 -- TBD Presentation 1.5 -- TBD Presentation 1.6 -- TBD
	05-03	project: Presentations, day 2 Presentation 2.0 -- TBD Presentation 2.1 -- TBD Presentation 2.2 -- TBD Presentation 2.3 -- TBD Presentation 2.4 -- TBD Presentation 2.5 -- TBD
	05-04	No class, reading day project 5: Project reflections due

Homework

• Homework 1, Due Wednesday February 8, 6pm Friday, February 10, 6pm.
• Homework 2, Due Wednesday March 1, 12pm.
• Homework 3, Due Wednesday March 24 Friday March 31st, 12pm.
• Homework 4, Due Friday April 14th, noon.
• Project 0, Due Wednesday March 22 in class
• Project 1 - goals, Due Friday March 31 end of day.
• Project 2 - outline, Due Friday April 7, end of class.
• Project 3 - results, Due Wednesday April 12, end of class.
• Project 4 - results, Due Wednesday April 19, end of day.
• Project 5 - slides, Due Wednesday April 26, beginning of class.
• Project 6 - reflections, Due Friday May 5 by 6pm.

Guidelines and files

• all homeworks should be typeset in LaTeX. For a template you may start with homework-netid-N.tex or overleaf project.

Final Presentations

The final presentation should focus on educating the audience with a clear statement of the problem (PDE) being looked at, a description of the method and its implementation, numerical results that highlight certain features of the study, and some reflective conclusions.

Your presentation should be 10 minutes long (!), with roughly 10 slides (depending on your content). Here is a rubric for the grading (equally weighted).

SP, Statement of problem

• Equations to be solved, including BCs and ICs if necessary. Connection to engineering/science problem if appropriate.

SA, Solution approach

• Discretization problem formulation, with justification. Why is this method of interest.

ID, Implementation details

• What details are needed to understand the implementation? What code(s) did you use?

R, Results

• What was the initial goal and did it succeed? What do you observe for this problem and discretization?

C, Conclusions

• What did you learn? What worked, what needs improvement, what are the next steps or future directions?

Books

Computing

We will be using Python with the libraries numpy, scipy and matplotlib for assignments. No other languages are permitted.

Python and Numpy Help

• Python tutorial
• Facts and myths about Python names and values
• Dive into Python 3
• Introduction to Python for Science
• The SciPy lectures
• The Numpy MedKit by Stéfan van der Walt
• The Numpy User Guide by Travis Oliphant
• Numpy/Scipy documentation
• More in this reddit thread
• An introduction to Numpy and SciPy
• 100 Numpy exercises

COVID and Attendance

While face coverings are not required in classrooms (current as of 01/17) we fully support your decision to wear one if you wish.

If you test positive for COVID, then you should not attend class.

If you have any cold-like symptoms or do not feel well, then you should not attend class, regardless of testing negative or positive for COVID.

In either case, your missed attendance due to illness will not impact your grade in the course and we will work with you to cover the material missed in class (via Zoom).