Numerical Methods for Partial Differential Equations

CS555 :: Spring 2024

• Class Time: Monday/Wednesday 11:00am-12:15pm Catalog
• Class Location: 2039 Campus Instructional Facility (CIF)
• Class URL: go.illinois.edu/cs555
• Slack: cs555-s24
• Instructor: Luke Olson
• Teaching Assistant: Alexey Voronin
• Office Hours: Thursdays 1-2pm and Fridays 4-5pm via zoom (NetID signin required)

About the Course

Are you interested in the numerical approximation of solutions to partial differential equations? Then this course is for you!

The course covers roughly three topics: the fundamentals of finite difference approximations, an introduction to finite volume schemes, and comprehensive look at finite element methods.

The course involves several assignments (usually bi-weekly) and a final project that we develop over the semester, culminating in a presentation. There is also a strong participation grade based on handouts and other in-class tasks. The tentative grade breakdown is:

• Homework 50
• Final Project 40
• Handouts/in-class activities 10 (we will be clear about these -- not all will be handed in)

This will be finalized in the first week of class.

The course assignments and examples in class will be in Python.

Lectures

Recorded Lectures: mediaspace.illinois.edu

Lecture	Date	Topic
	01-17	About the course, classifying PDEs, survey of methods Book Chapter 1
	01-22	Finite differencing for time dependent problems Book Sections 2.2, 3.1, 3.3, 5.1-5.3 05-advection-1d-template.ipynb  notes-20240122.pdf
	01-24	Convergence theory, Stability Book Sections 5.1-5.3 notes-20240124.pdf
	01-29	Stabilty, dispersion, and dissipation Book Sections 5.1-5.4 toeplitz.ipynb  notes-20240129.pdf
	01-31	Dispersion, and dissipation Book Sections 5.3-5.4 Scalar conservation laws 05-advection-ETBS-LW.ipynb  05-dispersion-and-dissipation.ipynb  notes-20240131.pdf
	02-05	Conservation laws, finite volume methods Book Sections 6.1-6.2 05-advection-ETBS-dissipation.ipynb  notes-20240205.pdf
	02-07	Finite Volume Methods Book sections 6.2-6.3 06-burgers-ETBS.ipynb  06-burgers-fv-1storder.ipynb  06-quasilinear-advection.py (raw) notes-20240207.pdf
	02-12	Godunov Schemes Book sections 6.3, 6.5 06-burgers-LF.ipynb  notes-20240212.pdf
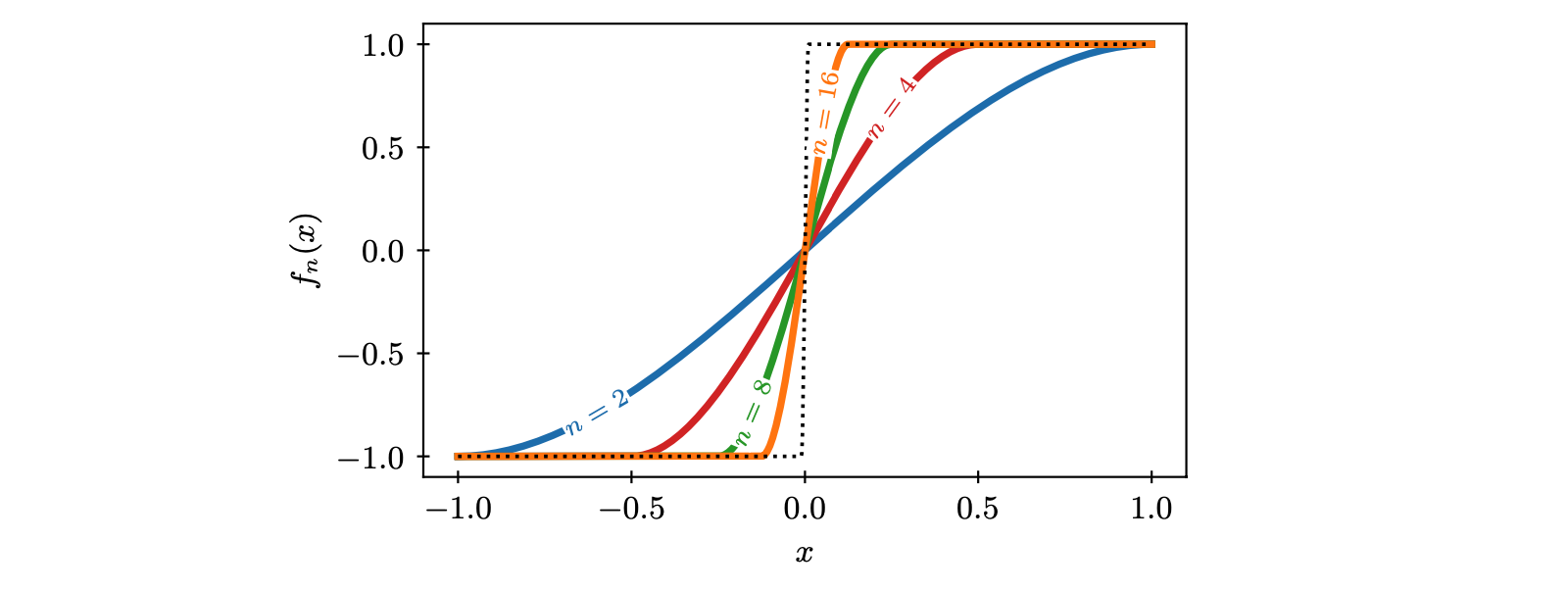
	02-14	Higher resolution and slope limiting Book sections 6.5 06-quasilinear-advection-linear-tvd.py (raw) 06-quasilinear-advection-linear.py (raw) 06-advection-constant.ipynb  06-advection-general.ipynb  notes-20240214.pdf
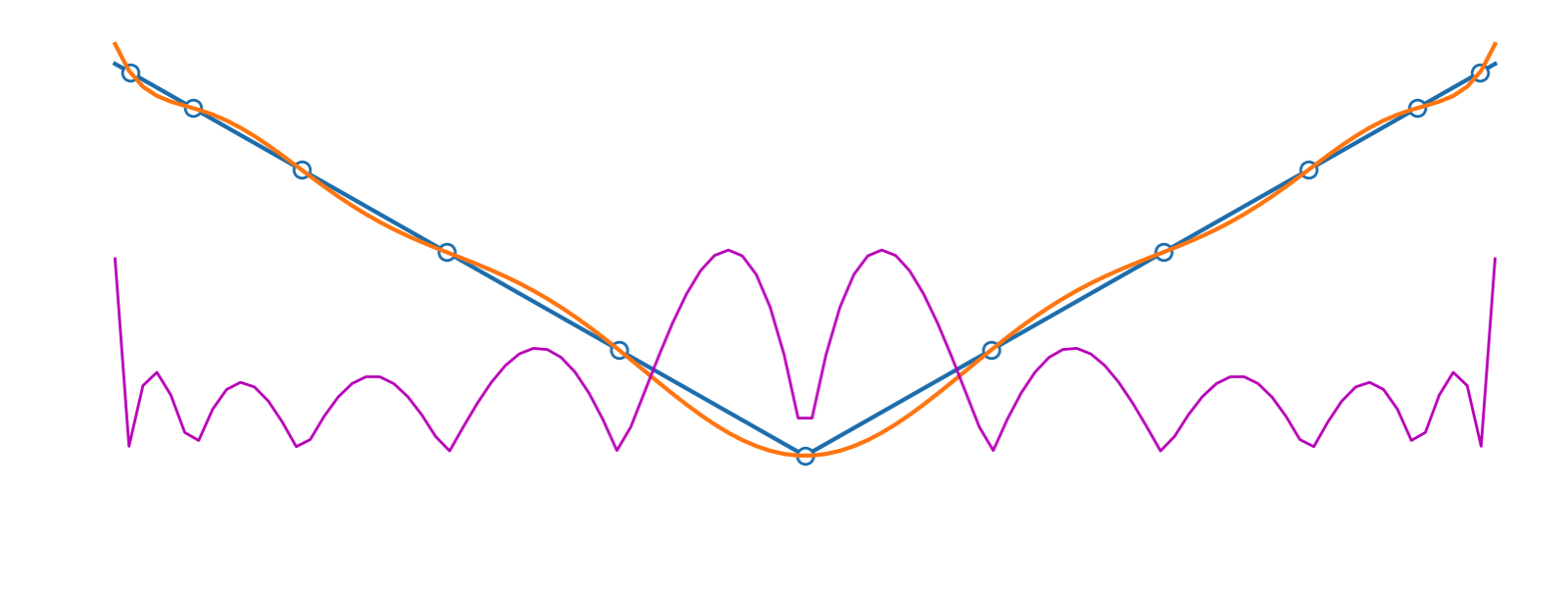
	02-19	Weak derivatives Book sections 4.1, 8.1 notes-20240219-ak.pdf
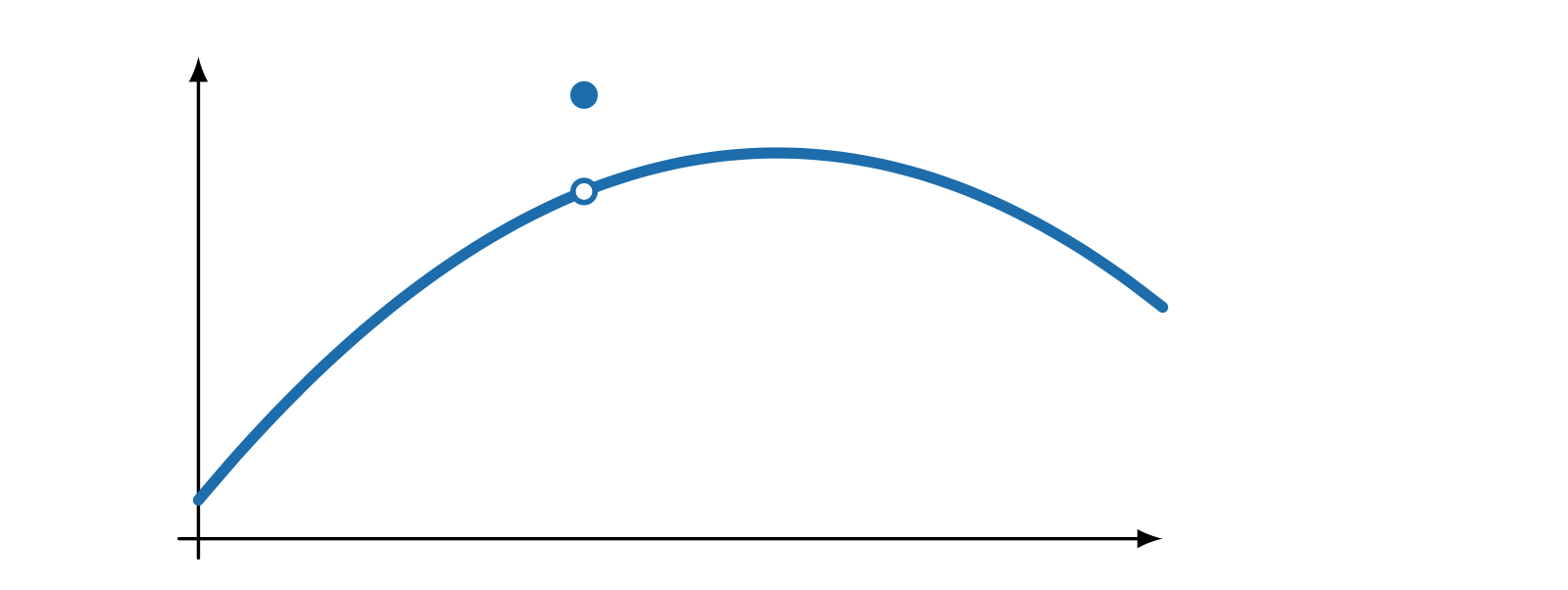
	02-21	Projections and weak problems Book sections 4.1 polynomial-approximation-template.ipynb  2-polynomial-approximation.ipynb  notes-20240221.pdf
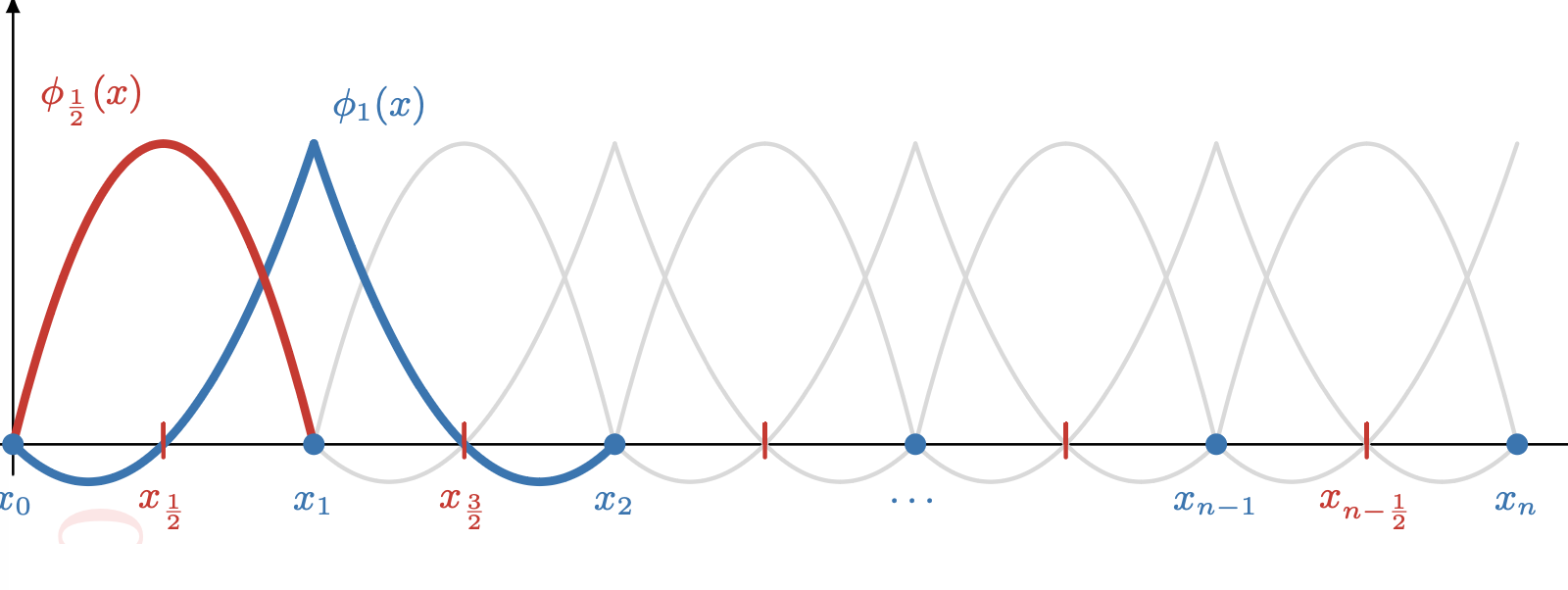
	02-26	Weak forms, Ritz-Galerkin, existence and uniqueness Book Section 4.1, 4.2 notes-20240226.pdf
	02-28	Finite element assembly Book section 4.4 04_fem_assembly_1d_starter.ipynb  04_fem_assembly_1d.ipynb  notes-20240228.pdf
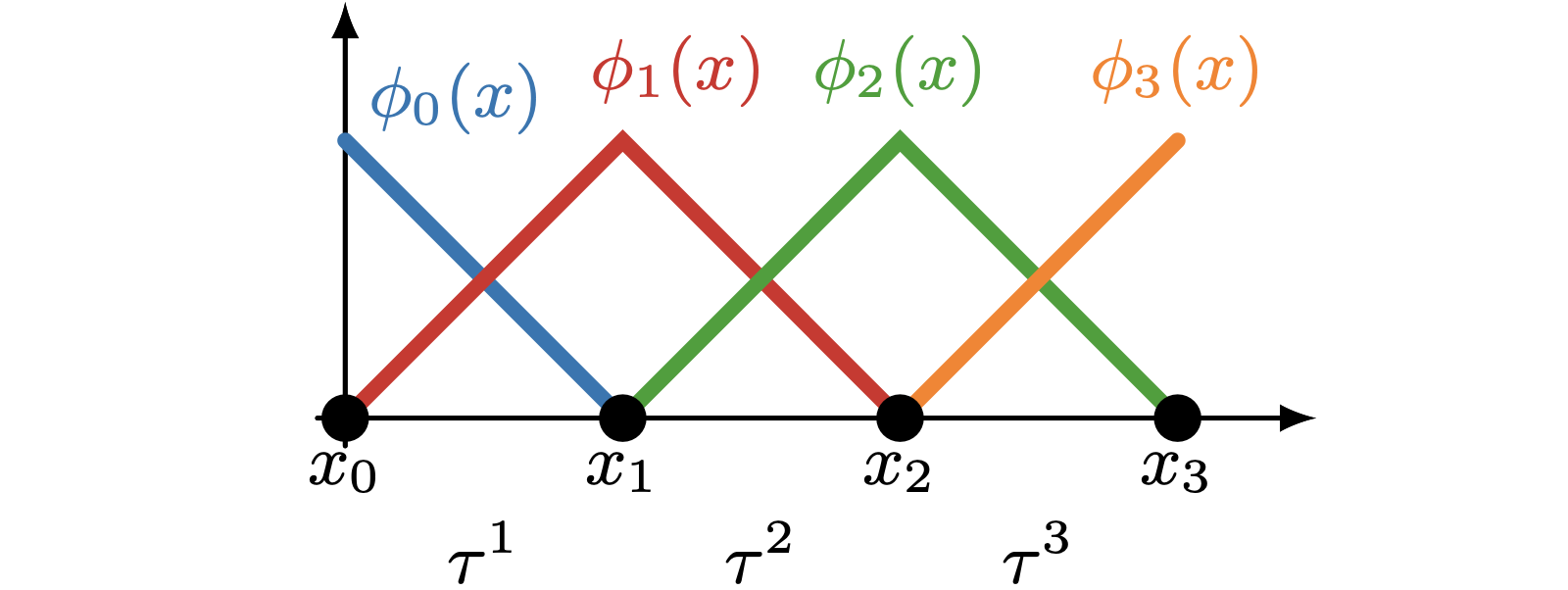	03-04	Finite element interpolant, approximation property Finite element assembly, 1d Read section 4.4 notes-20240304.pdf
	03-06	Various FE methods, from least-squares to Galerkin Book section 8.4 notes-20240306.pdf
	03-11	Spring Break
	03-13	Spring Break
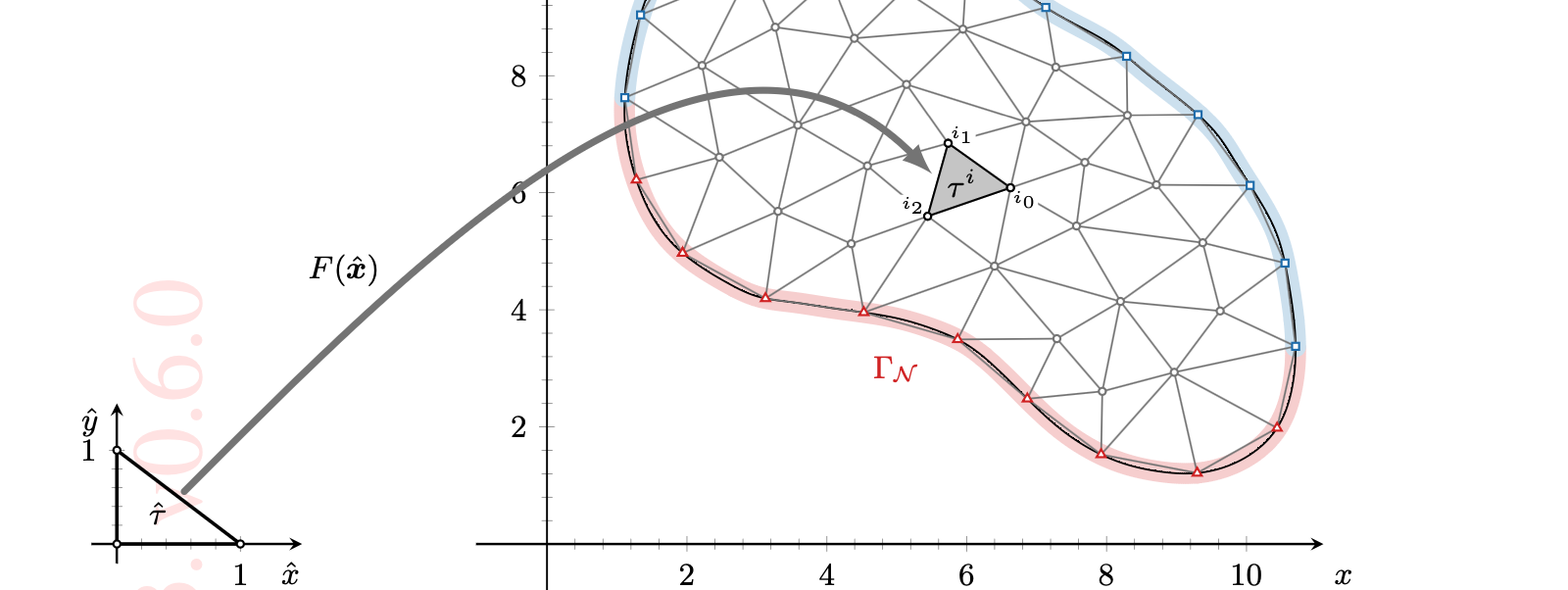	03-18	Finite element assembly in 2D Book section 8.4 08-fe-assembly-template.ipynb  notes-20240318.pdf
	03-20	Finite element assembly in 2D Book section 8.4 notes-20240320.pdf
	03-25	Introduction to Functional Anaylsis Book section 8.1 notes-20240325.pdf
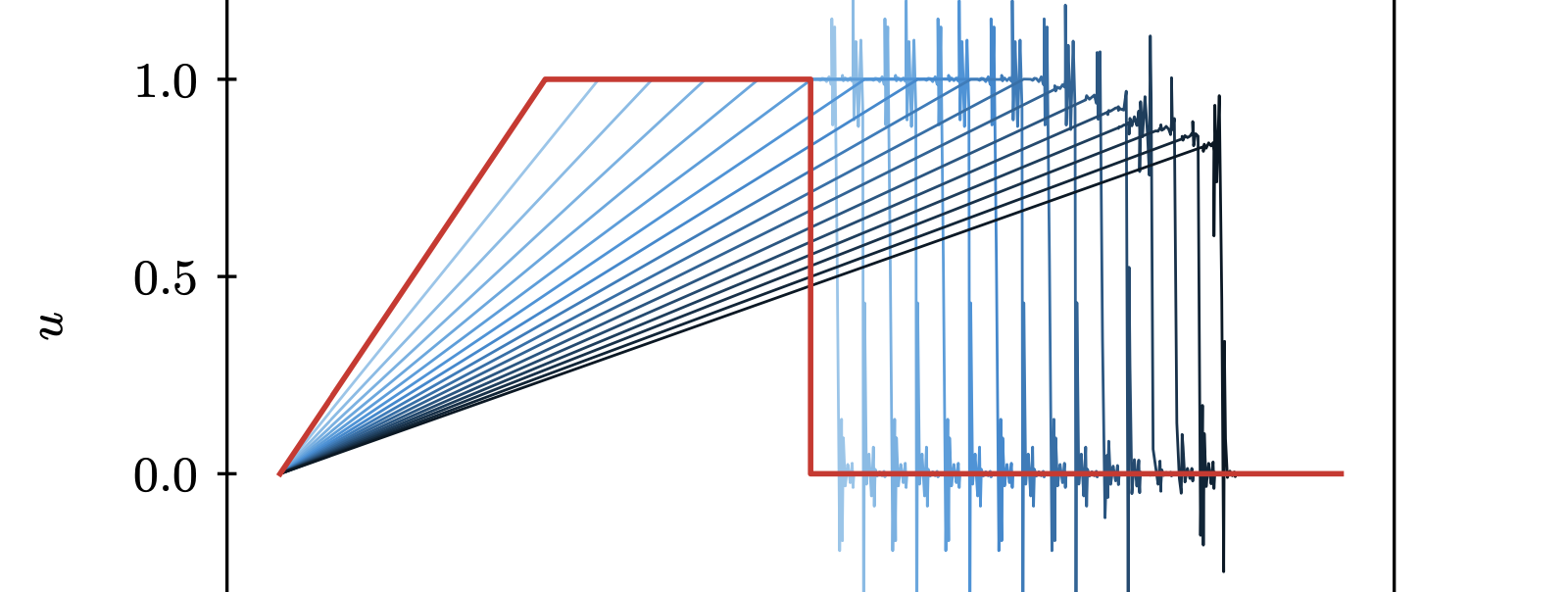
	03-27	An outline of theory, Lax-Milgram, and more Book section 8.2 notes-20240327.pdf
	04-01	Back to DG Book section 9.5 09-dg-todo.ipynb
	04-03	more DG 09-dg-todo.ipynb
	04-08	Least-squares finite elements Book section 10.5 09-dg.ipynb
	04-10	Least-squares FE
	04-15	Mixed order FE
	04-17	Advanced elements
	04-22	Presentations, day 0 555-presentation.pdf
	04-24	Presentations, day 1
	04-29	Presentations, day 2
	05-01	Presentations, day 3
	05-02	No class, reading day

Homework

• Homework 1, Due Wednesday February 7, 6pm.
• Homework 2, Due Friday February 23, 6pm.
• Homework 3, Released Wednesday February 28. Due Friday March 8, 6pm.
• Homework 4, Released Wednesday February March 20. Due Monday April 1st, 11am.

Guidelines and files:

• Homework Submission: All homework must be typeset using LaTeX. Use the provided templates to get started, available at homework-netid-N.tex or overleaf project.
• Figures: Make sure all figures are clearly labeled with axes, titles, legends, and captions. Each figure must be referenced and discussed within your text for full credit.
• Originality: Your submitted code and figures must be your own. If you use someone else's work, you must cite it.
• Code-Based Problems: To receive points for problems involving code, your code must reproduce the reported figures and data. No points will be awarded for the Codes that do not generate the reported results.
• Debugging Efforts: If you encounter issues that prevent your code from working as expected, detailed descriptions of your debugging attempts can earn you partial credit.

Final Project

The goal of the final project is to develop your own mini app -- a short computational example of some phenomenon in numerical PDEs. This can be related to any of the topics covered, from finite differencing to finite volume methods to finite element methods. An overarching goal of your mini app is to educate your peers on some nuanced aspect of the topics we have covered (or have skipped).

Your deliverables for the project will be a functioning Jupyter notebook, with an embeddeed description, discussion, and guide for the audience. In addition, you will present an overview of up to five minutes (with slides).

The mini app should rely only on standard Python, along with numpy, scipy, and matplotlib. If you strongly feel that you should use additional packages, please obtain prior approval.

The rubrics for the mini app are as follows.

SP, Statement of problem

• What is the problem that you are looking at? What is the is point of the the mini app? What interesting aspect of numerical PDEs does your mini app highlight?
• Is the problem clear? Have you provided enough background information for the audience to follow?

ID, Implementation details

• Is your example well documented?
• Is your mini app reproducible with minimal effort?
• What details are needed to understand the implementation?
• Is your Python code style clean and Pythonic? (see for example, The Zen of Pytyhon, https://peps.python.org/pep-0020/)

R, Results

• Do your results highlight the overarching goal of your mini app?
• What do you observe for this problem and discretization, for example?
• Are your results clear? Do you label important details? Do you use relevant and consistent color schemes?
• Carefully select which visualizations to show. We do not need to see everything, only figures that highlight some aspect of the goal of your mini app.

C, Reflections

• What did you learn? What worked, what needs improvement, what are the next steps or future directions?
• Provide a list of future directions at the end of your app -- what could be looked at next and what are some of the limitations of your implementation?

Slides should focus on

• (3) Do you have a clear summary and goals of your miniapp?
• (2) Do you provide a sufficient level of detail in showing off your mini app?
• (2) Do you highlight a few (but not all) of the results in your mini app?
• (3) Is your presentation practiced and on time? Is your slide deck of high quality?

Code details.

• The code should be your own. If you use someone else's function or module, then it should be clearly attributed and the license should conform to your license.
• License. Ideally it would be useful if your mini app is released as open source.
• Your notebook should be named miniapp_topic.ipynb. No spaces or dashes.

COVID and Attendance

While face coverings are not required in classrooms (current as of 12/20/2023) we fully support your decision to wear one if you wish.

If you test positive for COVID, then you should not attend class.

If you have any cold-like symptoms or do not feel well, then you should not attend class, regardless of testing negative or positive for COVID.

In either case, your missed attendance due to illness will not impact your grade in the course and we will work with you to cover the material missed in class (via Zoom).